Note
Go to the end to download the full example code or to run this example in your browser via Binder.
Challenge 2: Predicting the p-factor from EEG#
#
Preliminary notes
Before we begin, I just want to make a deal with you, ok? This is a community competition with a strong open-source foundation. When I say open-source, I mean volunteer work.
So, if you see something that does not work or could be improved, first, please be kind, and we will fix it together on GitHub, okay?
The entire decoding community will only go further when we stop solving the same problems over and over again, and it starts working together.
#
Overview
The psychopathology factor (P-factor) is a widely recognized construct in mental health research, representing a common underlying dimension of psychopathology across various disorders. Currently, the P-factor is often assessed using self-report questionnaires or clinician ratings, which can be subjective, prone to bias, and time-consuming. The Challenge 2 consists of developing a model to predict the P-factor from EEG recordings.
The challenge encourages learning physiologically meaningful signal representations and discovery of reproducible biomarkers. Models of any size should emphasize robust, interpretable features that generalize across subjects, sessions, and acquisition sites.
Unlike a standard in-distribution classification task, this regression problem stresses out-of-distribution robustness and extrapolation. The goal is not only to minimize error on seen subjects, but also to transfer effectively to unseen data. Ensure the dataset is available locally. If not, see the dataset download guide.
Contents of this start kit
Note
If you need additional explanations on the EEGChallengeDataset class, dataloading, braindecode’s deep learning models, or brain decoding in general, please refer to the start-kit of challenge 1 which delves deeper into these topics.
More contents will be released during the competition inside the
eegdashexamples webpage.Prerequisites
The tutorial assumes prior knowledge of:
Standard neural network architectures (e.g., CNNs)
Optimization by batch gradient descent and backpropagation
Overfitting, early stopping, and regularization
Some knowledge of PyTorch
Basic familiarity with EEG and preprocessing
An appreciation for open-source work :)
Install dependencies on Colab
Note
These installs are optional; skip on local environments where you already have the dependencies installed.
pip install eegdash
Imports
from pathlib import Path
import math
import os
import random
import torch
from torch.utils.data import DataLoader
from torch import optim
from torch.nn.functional import l1_loss
from braindecode.preprocessing import create_fixed_length_windows
from braindecode.datasets.base import EEGWindowsDataset, BaseConcatDataset, BaseDataset
from braindecode.models import EEGNeX
from eegdash import EEGChallengeDataset
from eegdash.paths import get_default_cache_dir
#
Warning
In case of Colab, before starting, make sure you’re on a GPU instance for faster training! If running on Google Colab, please request a GPU runtime by clicking Runtime/Change runtime type in the top bar menu, then selecting ‘T4 GPU’ under ‘Hardware accelerator’.
Identify whether a CUDA-enabled GPU is available
device = "cuda" if torch.cuda.is_available() else "cpu"
if device == "cuda":
msg = "CUDA-enabled GPU found. Training should be faster."
else:
msg = (
"No GPU found. Training will be carried out on CPU, which might be "
"slower.\n\nIf running on Google Colab, you can request a GPU runtime by"
" clicking\n`Runtime/Change runtime type` in the top bar menu, then "
"selecting 'T4 GPU'\nunder 'Hardware accelerator'."
)
print(msg)
#
No GPU found. Training will be carried out on CPU, which might be slower.
If running on Google Colab, you can request a GPU runtime by clicking
`Runtime/Change runtime type` in the top bar menu, then selecting 'T4 GPU'
under 'Hardware accelerator'.
Understanding the P-factor regression task
The psychopathology factor (P-factor) is a widely recognized construct in mental health research, representing a common underlying dimension of psychopathology across various disorders. The P-factor is thought to reflect the shared variance among different psychiatric conditions, suggesting that individuals with higher P-factor scores may be more vulnerable to a range of mental health issues. Currently, the P-factor is often assessed using self-report questionnaires or clinician ratings, which can be subjective, prone to bias, and time-consuming. In the dataset of this challenge, the P-factor was assessed using the Child Behavior Checklist (CBCL) McElroy et al., (2017).
The goal of Challenge 2 is to develop a model to predict the P-factor from EEG recordings. The feasibility of using EEG data for this purpose is still an open question. The solution may involve finding meaningful representations of the EEG data that correlate with the P-factor scores. The challenge encourages learning physiologically meaningful signal representations and discovery of reproducible biomarkers. If contestants are successful in this task, it could pave the way for more objective and efficient assessments of the P-factor in clinical settings.
Define local path and (down)load the data
In this challenge 2 example, we load the EEG 2025 release using EEGChallengeDataset. Note: in this example notebook, we load the contrast change detection task from one mini release only as an example. Naturally, you are encouraged to train your models on all complete releases, using data from all the tasks you deem relevant.
The first step is to define the cache folder! Match tests’ cache layout under ~/eegdash_cache/eeg_challenge_cache
DATA_DIR = Path(get_default_cache_dir()).resolve()
# Creating the path if it does not exist
DATA_DIR.mkdir(parents=True, exist_ok=True)
# We define the list of releases to load.
# Here, only release 5 is loaded.
release_list = ["R5"]
all_datasets_list = [
EEGChallengeDataset(
release=release,
task="contrastChangeDetection",
mini=True,
description_fields=[
"subject",
"session",
"run",
"task",
"age",
"gender",
"sex",
"p_factor",
],
cache_dir=DATA_DIR,
)
for release in release_list
]
print("Datasets loaded")
sub_rm = ["NDARWV769JM7"]
#
╭────────────────────── EEG 2025 Competition Data Notice ──────────────────────╮
│ This object loads the HBN dataset that has been preprocessed for the EEG │
│ Challenge: │
│ * Downsampled from 500Hz to 100Hz │
│ * Bandpass filtered (0.5-50 Hz) │
│ │
│ For full preprocessing applied for competition details, see: │
│ https://github.com/eeg2025/downsample-datasets │
│ │
│ The HBN dataset have some preprocessing applied by the HBN team: │
│ * Re-reference (Cz Channel) │
│ │
│ IMPORTANT: The data accessed via `EEGChallengeDataset` is NOT identical to │
│ what you get from EEGDashDataset directly. │
│ If you are participating in the competition, always use │
│ `EEGChallengeDataset` to ensure consistency with the challenge data. │
╰──────────────────────── Source: EEGChallengeDataset ─────────────────────────╯
Datasets loaded
Combine the datasets into a single one
Here, we combine the datasets from the different releases into a single
BaseConcatDataset object.
%%
all_datasets = BaseConcatDataset(all_datasets_list)
print(all_datasets.description)
for ds in all_datasets_list:
ds.download_all(n_jobs=os.cpu_count())
#
subject run ... seqlearning8target symbolsearch
0 NDARAH793FBF 2 ... available available
1 NDARAH793FBF 3 ... available available
2 NDARAH793FBF 1 ... available available
3 NDARAJ689BVN 3 ... unavailable available
4 NDARAJ689BVN 2 ... unavailable available
5 NDARAJ689BVN 1 ... unavailable available
6 NDARAP785CTE 1 ... available available
7 NDARAP785CTE 3 ... available available
8 NDARAP785CTE 2 ... available available
9 NDARAU708TL8 1 ... available available
10 NDARAU708TL8 2 ... available available
11 NDARAU708TL8 3 ... available available
12 NDARBE091BGD 3 ... unavailable available
13 NDARBE091BGD 2 ... unavailable available
14 NDARBE091BGD 1 ... unavailable available
15 NDARBE103DHM 1 ... available available
16 NDARBE103DHM 2 ... available available
17 NDARBE103DHM 3 ... available available
18 NDARBF851NH6 3 ... available available
19 NDARBF851NH6 2 ... available available
20 NDARBF851NH6 1 ... available available
21 NDARBH228RDW 1 ... available available
22 NDARBH228RDW 2 ... available available
23 NDARBH228RDW 3 ... available available
24 NDARBJ674TVU 1 ... unavailable available
25 NDARBJ674TVU 3 ... unavailable available
26 NDARBJ674TVU 2 ... unavailable available
27 NDARBM433VER 1 ... available available
28 NDARBM433VER 2 ... available available
29 NDARBM433VER 3 ... available available
30 NDARCA740UC8 2 ... available available
31 NDARCA740UC8 3 ... available available
32 NDARCA740UC8 1 ... available available
33 NDARCU633GCZ 1 ... available available
34 NDARCU633GCZ 3 ... available available
35 NDARCU633GCZ 2 ... available available
36 NDARCU736GZ1 2 ... unavailable available
37 NDARCU736GZ1 3 ... unavailable available
38 NDARCU736GZ1 1 ... unavailable available
39 NDARCU744XWL 1 ... available available
40 NDARCU744XWL 3 ... available available
41 NDARCU744XWL 2 ... available available
42 NDARDC843HHM 3 ... available available
43 NDARDC843HHM 2 ... available available
44 NDARDC843HHM 1 ... available available
45 NDARDH086ZKK 2 ... available available
46 NDARDH086ZKK 3 ... available available
47 NDARDH086ZKK 1 ... available available
48 NDARDL305BT8 1 ... available available
49 NDARDL305BT8 2 ... available available
50 NDARDL305BT8 3 ... available available
51 NDARDU853XZ6 3 ... unavailable available
52 NDARDU853XZ6 2 ... unavailable available
53 NDARDU853XZ6 1 ... unavailable available
54 NDARDV245WJG 3 ... unavailable available
55 NDARDV245WJG 2 ... unavailable available
56 NDARDV245WJG 1 ... unavailable available
57 NDAREC480KFA 1 ... available available
58 NDAREC480KFA 2 ... available available
59 NDAREC480KFA 3 ... available available
[60 rows x 26 columns]
Inspect your data
We can check what is inside the dataset consuming the MNE-object inside the Braindecode dataset.
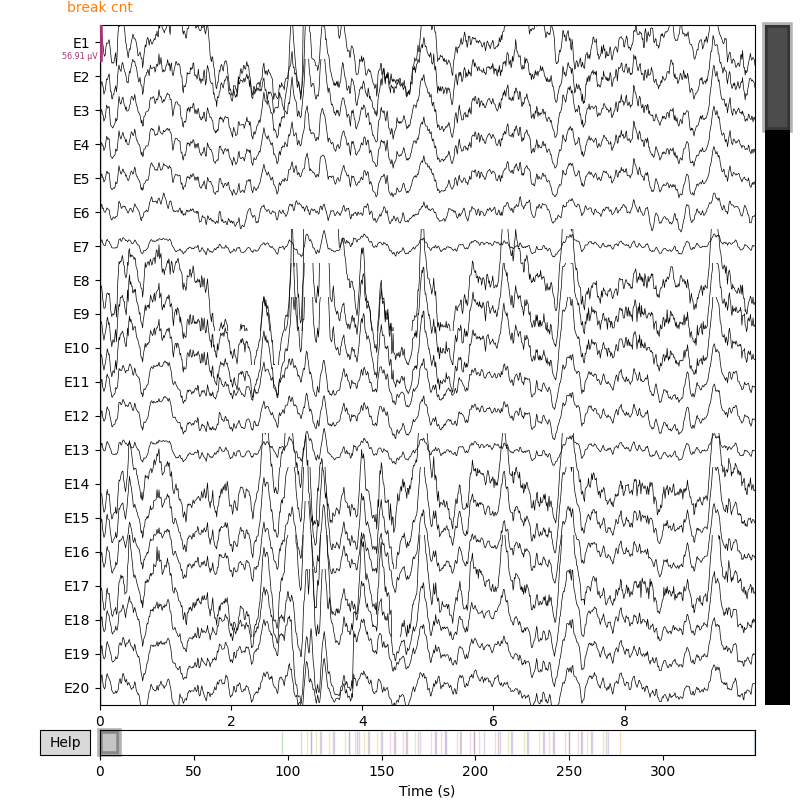
The following snippet, if uncommented, will show the first 10 seconds of the raw EEG signal. We can also inspect the data further by looking at the events and annotations. We strongly recommend you to take a look into the details and check how the events are structured.
raw = all_datasets.datasets[0].raw # mne.io.Raw object
print(raw.info)
raw.plot(duration=10, scalings="auto", show=True)
print(raw.annotations)
SFREQ = 100
#
<Info | 9 non-empty values
bads: []
ch_names: E1, E2, E3, E4, E5, E6, E7, E8, E9, E10, E11, E12, E13, E14, ...
chs: 129 EEG
custom_ref_applied: False
highpass: 0.0 Hz
line_freq: 60.0
lowpass: 50.0 Hz
meas_date: 2025-08-19 00:06:17 UTC
nchan: 129
projs: []
sfreq: 100.0 Hz
subject_info: <subject_info | >
>
Using matplotlib as 2D backend.
<Annotations | 74 segments: 9999 (1), break cnt (1), ...>
Wrap the data into a PyTorch-compatible dataset
The class below defines a dataset wrapper that will extract 2-second windows, uniformly sampled over the whole signal. In addition, it will add useful information about the extracted windows, such as the p-factor, the subject or the task.
class DatasetWrapper(BaseDataset):
def __init__(self, dataset: EEGWindowsDataset, crop_size_samples: int, seed=None):
self.dataset = dataset
self.crop_size_samples = crop_size_samples
self.rng = random.Random(seed)
def __len__(self):
return len(self.dataset)
def __getitem__(self, index):
X, _, crop_inds = self.dataset[index]
# P-factor label:
p_factor = self.dataset.description["p_factor"]
p_factor = float(p_factor)
# Additional information:
infos = {
"subject": self.dataset.description["subject"],
"sex": self.dataset.description["sex"],
"age": float(self.dataset.description["age"]),
"task": self.dataset.description["task"],
"session": self.dataset.description.get("session", None) or "",
"run": self.dataset.description.get("run", None) or "",
}
# Randomly crop the signal to the desired length:
i_window_in_trial, i_start, i_stop = crop_inds
assert i_stop - i_start >= self.crop_size_samples, f"{i_stop=} {i_start=}"
start_offset = self.rng.randint(0, i_stop - i_start - self.crop_size_samples)
i_start = i_start + start_offset
i_stop = i_start + self.crop_size_samples
X = X[:, start_offset : start_offset + self.crop_size_samples]
return X, p_factor, (i_window_in_trial, i_start, i_stop), infos
# We filter out certain recordings, create fixed length windows and finally make use of our `DatasetWrapper`.
Filter out recordings that are too short or missing p_factor
all_datasets = BaseConcatDataset(
[
ds
for ds in all_datasets.datasets
if ds.description.subject not in sub_rm
and ds.raw.n_times >= 4 * SFREQ
and len(ds.raw.ch_names) == 129
and "p_factor" in ds.description
and ds.description["p_factor"] is not None
and not math.isnan(ds.description["p_factor"])
]
)
# Create 4-seconds windows with 2-seconds stride
windows_ds = create_fixed_length_windows(
all_datasets,
window_size_samples=4 * SFREQ,
window_stride_samples=2 * SFREQ,
drop_last_window=True,
)
# Wrap each sub-dataset in the windows_ds
windows_ds = BaseConcatDataset(
[DatasetWrapper(ds, crop_size_samples=2 * SFREQ) for ds in windows_ds.datasets]
)
#
Inspect the label distribution
import numpy as np
from skorch.helper import SliceDataset
y_label = np.array(list(SliceDataset(windows_ds, 1)))
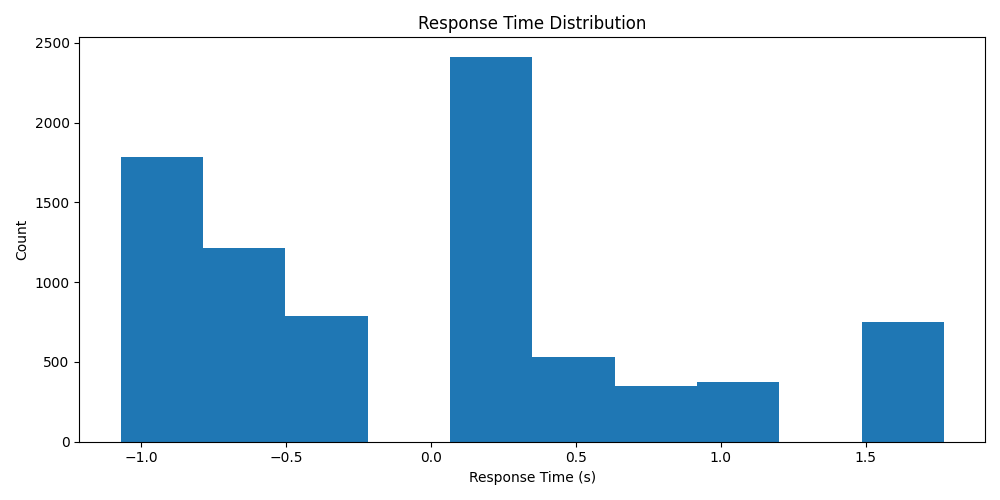
# Plot histogram of the response times with matplotlib
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(10, 5))
ax.hist(y_label)
ax.set_title("Response Time Distribution")
ax.set_xlabel("Response Time (s)")
ax.set_ylabel("Count")
plt.tight_layout()
plt.show()
#
Define, train and save a model
Now we have our pytorch dataset necessary for the training!
Below, we define a simple EEGNeX model from Braindecode. All the braindecode models expect the input to be of shape (batch_size, n_channels, n_times) and have a test coverage about the behavior of the model. However, you can use any pytorch model you want.
Initialize model
model = EEGNeX(n_chans=129, n_outputs=1, n_times=2 * SFREQ).to(device)
# Specify optimizer
optimizer = optim.Adamax(params=model.parameters(), lr=0.002)
print(model)
# Finally, we can train our model. Here we define a simple training loop using pure PyTorch.
# In this example, we only train for a single epoch. Feel free to increase the number of epochs.
# Create PyTorch Dataloader
num_workers = (
0 # Set num_workers to 0 to avoid multiprocessing issues in notebooks/tutorials.
)
dataloader = DataLoader(
windows_ds, batch_size=128, shuffle=True, num_workers=num_workers
)
n_epochs = 1
# Train model for 1 epoch
for epoch in range(n_epochs):
for idx, batch in enumerate(dataloader):
# Reset gradients
optimizer.zero_grad()
# Unpack the batch
X, y, crop_inds, infos = batch
X = X.to(dtype=torch.float32, device=device)
y = y.to(dtype=torch.float32, device=device).unsqueeze(1)
# Forward pass
y_pred = model(X)
# Compute loss
loss = l1_loss(y_pred, y)
print(f"Epoch {0} - step {idx}, loss: {loss.item()}")
# Gradient backpropagation
loss.backward()
optimizer.step()
# Finally, we can save the model for later use
torch.save(model.state_dict(), "weights_challenge_2.pt")
print("Model saved as 'weights_challenge_2.pt'")
================================================================================================================================================================
Layer (type (var_name):depth-idx) Input Shape Output Shape Param # Kernel Shape
================================================================================================================================================================
EEGNeX (EEGNeX) [1, 129, 200] [1, 1] -- --
├─Sequential (block_1): 1-1 [1, 129, 200] [1, 8, 129, 200] -- --
│ └─Rearrange (0): 2-1 [1, 129, 200] [1, 1, 129, 200] -- --
│ └─Conv2d (1): 2-2 [1, 1, 129, 200] [1, 8, 129, 200] 512 [1, 64]
│ └─BatchNorm2d (2): 2-3 [1, 8, 129, 200] [1, 8, 129, 200] 16 --
├─Sequential (block_2): 1-2 [1, 8, 129, 200] [1, 32, 129, 200] -- --
│ └─Conv2d (0): 2-4 [1, 8, 129, 200] [1, 32, 129, 200] 16,384 [1, 64]
│ └─BatchNorm2d (1): 2-5 [1, 32, 129, 200] [1, 32, 129, 200] 64 --
├─Sequential (block_3): 1-3 [1, 32, 129, 200] [1, 64, 1, 50] -- --
│ └─ParametrizedConv2dWithConstraint (0): 2-6 [1, 32, 129, 200] [1, 64, 1, 200] -- [129, 1]
│ │ └─ModuleDict (parametrizations): 3-1 -- -- 8,256 --
│ └─BatchNorm2d (1): 2-7 [1, 64, 1, 200] [1, 64, 1, 200] 128 --
│ └─ELU (2): 2-8 [1, 64, 1, 200] [1, 64, 1, 200] -- --
│ └─AvgPool2d (3): 2-9 [1, 64, 1, 200] [1, 64, 1, 50] -- [1, 4]
│ └─Dropout (4): 2-10 [1, 64, 1, 50] [1, 64, 1, 50] -- --
├─Sequential (block_4): 1-4 [1, 64, 1, 50] [1, 32, 1, 50] -- --
│ └─Conv2d (0): 2-11 [1, 64, 1, 50] [1, 32, 1, 50] 32,768 [1, 16]
│ └─BatchNorm2d (1): 2-12 [1, 32, 1, 50] [1, 32, 1, 50] 64 --
├─Sequential (block_5): 1-5 [1, 32, 1, 50] [1, 48] -- --
│ └─Conv2d (0): 2-13 [1, 32, 1, 50] [1, 8, 1, 50] 4,096 [1, 16]
│ └─BatchNorm2d (1): 2-14 [1, 8, 1, 50] [1, 8, 1, 50] 16 --
│ └─ELU (2): 2-15 [1, 8, 1, 50] [1, 8, 1, 50] -- --
│ └─AvgPool2d (3): 2-16 [1, 8, 1, 50] [1, 8, 1, 6] -- [1, 8]
│ └─Dropout (4): 2-17 [1, 8, 1, 6] [1, 8, 1, 6] -- --
│ └─Flatten (5): 2-18 [1, 8, 1, 6] [1, 48] -- --
├─ParametrizedLinearWithConstraint (final_layer): 1-6 [1, 48] [1, 1] 1 --
│ └─ModuleDict (parametrizations): 2-19 -- -- -- --
│ │ └─ParametrizationList (weight): 3-2 -- [1, 48] 48 --
================================================================================================================================================================
Total params: 62,353
Trainable params: 62,353
Non-trainable params: 0
Total mult-adds (Units.MEGABYTES): 437.76
================================================================================================================================================================
Input size (MB): 0.10
Forward/backward pass size (MB): 16.65
Params size (MB): 0.22
Estimated Total Size (MB): 16.97
================================================================================================================================================================
Epoch 0 - step 0, loss: 0.6607961058616638
Epoch 0 - step 1, loss: 0.658185601234436
Epoch 0 - step 2, loss: 0.7199245691299438
Epoch 0 - step 3, loss: 0.6543059349060059
Epoch 0 - step 4, loss: 0.6631066799163818
Epoch 0 - step 5, loss: 0.6073415279388428
Epoch 0 - step 6, loss: 0.6869580745697021
Epoch 0 - step 7, loss: 0.6830250024795532
Epoch 0 - step 8, loss: 0.695357620716095
Epoch 0 - step 9, loss: 0.6525446176528931
Epoch 0 - step 10, loss: 0.6397525668144226
Epoch 0 - step 11, loss: 0.6074527502059937
Epoch 0 - step 12, loss: 0.6190057992935181
Epoch 0 - step 13, loss: 0.6578781604766846
Epoch 0 - step 14, loss: 0.6191129684448242
Epoch 0 - step 15, loss: 0.6367197036743164
Epoch 0 - step 16, loss: 0.6051433086395264
Epoch 0 - step 17, loss: 0.6225818991661072
Epoch 0 - step 18, loss: 0.6002963185310364
Epoch 0 - step 19, loss: 0.640442967414856
Epoch 0 - step 20, loss: 0.7045203447341919
Epoch 0 - step 21, loss: 0.6855034232139587
Epoch 0 - step 22, loss: 0.6466516852378845
Epoch 0 - step 23, loss: 0.6700730919837952
Epoch 0 - step 24, loss: 0.5806247591972351
Epoch 0 - step 25, loss: 0.580946147441864
Epoch 0 - step 26, loss: 0.6617522239685059
Epoch 0 - step 27, loss: 0.7205257415771484
Epoch 0 - step 28, loss: 0.6667196154594421
Epoch 0 - step 29, loss: 0.7113224864006042
Epoch 0 - step 30, loss: 0.6052795648574829
Epoch 0 - step 31, loss: 0.7111648321151733
Epoch 0 - step 32, loss: 0.7174273729324341
Epoch 0 - step 33, loss: 0.5936117768287659
Epoch 0 - step 34, loss: 0.6203186511993408
Epoch 0 - step 35, loss: 0.6810719966888428
Epoch 0 - step 36, loss: 0.6376907825469971
Epoch 0 - step 37, loss: 0.6816781759262085
Epoch 0 - step 38, loss: 0.6054810285568237
Epoch 0 - step 39, loss: 0.6359142065048218
Epoch 0 - step 40, loss: 0.6956772804260254
Epoch 0 - step 41, loss: 0.6594623327255249
Epoch 0 - step 42, loss: 0.6123723983764648
Epoch 0 - step 43, loss: 0.6944264769554138
Epoch 0 - step 44, loss: 0.5808399319648743
Epoch 0 - step 45, loss: 0.6454795002937317
Epoch 0 - step 46, loss: 0.6258784532546997
Epoch 0 - step 47, loss: 0.6365463137626648
Epoch 0 - step 48, loss: 0.6176670789718628
Epoch 0 - step 49, loss: 0.6377511620521545
Epoch 0 - step 50, loss: 0.6832955479621887
Epoch 0 - step 51, loss: 0.6538573503494263
Epoch 0 - step 52, loss: 0.6113529205322266
Epoch 0 - step 53, loss: 0.6567574739456177
Epoch 0 - step 54, loss: 0.616517186164856
Epoch 0 - step 55, loss: 0.6300942301750183
Epoch 0 - step 56, loss: 0.6153266429901123
Epoch 0 - step 57, loss: 0.6781671047210693
Epoch 0 - step 58, loss: 0.6319180130958557
Epoch 0 - step 59, loss: 0.6302580833435059
Epoch 0 - step 60, loss: 0.6436354517936707
Epoch 0 - step 61, loss: 0.6305228471755981
Epoch 0 - step 62, loss: 0.6496596932411194
Epoch 0 - step 63, loss: 0.6873840093612671
Epoch 0 - step 64, loss: 0.7451661229133606
Model saved as 'weights_challenge_2.pt'
Total running time of the script: (6 minutes 45.935 seconds)
Estimated memory usage: 1742 MB